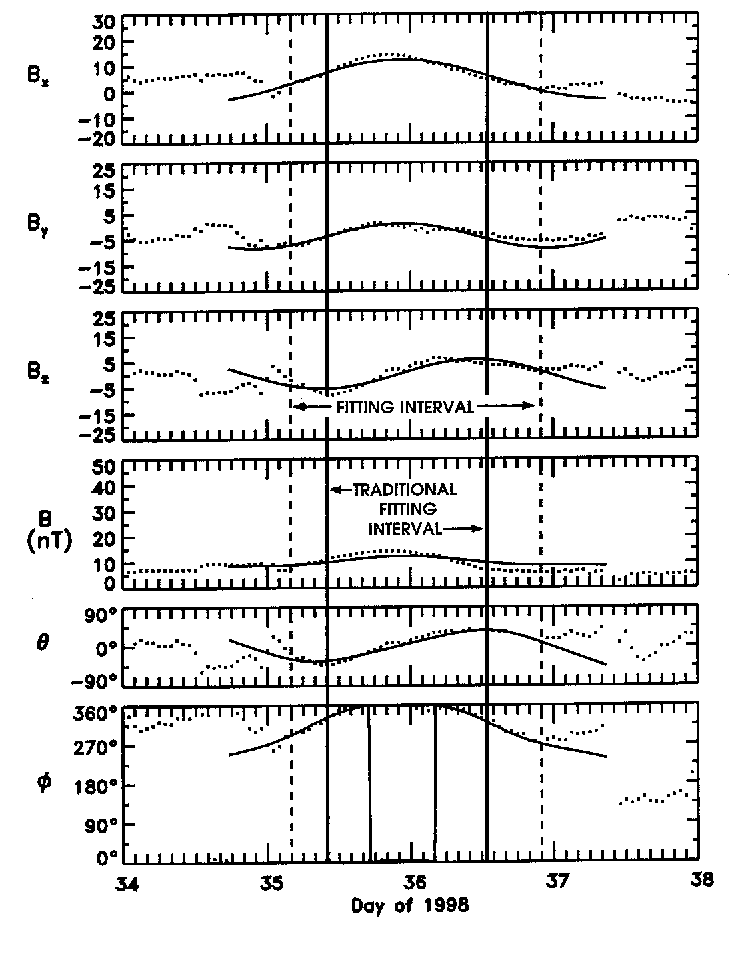

The figure shows the results of fitting the 7 parameter force free magnetic cloud model to the interplanetary magnetic field observations in the "fitting interval" from Feb 4 (Day 035), hour 4 to Feb 5, hour 22, 1998; the boundaries of this 43 hour interval (which includes the cloud's end-points) are denoted by the vertical dashed lines. For symmetrical cases like this one the "traditional fitting interval" (denoted by the heavy solid vertical lines) is chosen such that the start-time is at the minimum of theta (or maximum) and the end-time is at the maximum (or minimum) of theta. By choosing the cloud's fitting interval in this traditional way, for such a case where the axis of the cloud (or magnetic flux rope) is in or near the Ecliptic plane, as this one is, we are assured that the total magnetic field of the flux rope on the boundary is purely an azimuthal field and that the axial field within the flux rope is unidirectional. These are reasonable assumptions for the usual perception of a magnetic flux rope in the solar wind. That would have given a 28 hour fitting-interval. In this Feb 4th case, however, the model appears to do an excellent job of fitting the directions of the field, given by theta and phi, over a non-traditionally large fitting-interval, the 43 hour interval. See the Table of fit-parameters for this case; it yields one of the very best chi-squared values of any magnetic cloud studied. The obvious deviation of the model field from the observations at and beyond the vertical dashed lines, on both sides, clearly seen for Bx, Bz, field longitude and latitude, argues for the choice of these as boundary times. This kind of deviation is not seen at the traditional fitting interval boundaries.
In support of these times fo r the boundary of the flux rope/magnetic cloud, the WIND-SWE data (K. Ogilvie/P.I.), in particular the markedly depressed proton thermal velocity observed between these times compared to average temperatures in the solar wind, satisfies the definition of a magnetic cloud, with one brief 2-hour period of violation within the structure. It is interesting to note, and somewhat surprising also, that when the much shorter, 28 hour, interval is used for the fitting (results not shown) the estimation of the size of the diameter of the rope's cross-section is about the same as was obtained for the 42 hour interval's fit. But the longer interval, in fact, gave slightly better all around results. This finding of an excellent fit for a non-traditionally large fitting-interval deserves further study. It appears that the model holds for more-or-less symmetrical regions (in time) outside of the core (unidirectional axial) field region for this and possibly some other interplanetary magnetic clouds, and that this is apparently not a violation of the force free model, but is more of a change in our usual way of defining flux rope boundary conditions. The change in direction of the axial field then occurs at an imagined boundary between the core of the flux rope (our traditional "flux rope") and what may be thought of as an annulus around the core, all of which may be thought of as a new kind of flux rope structure. This is all preliminary.