Transformation from Solar Ecliptic Coordinates to a Magnetic Cloud Coordinate System, where the Cloud Axis is the New X-axis


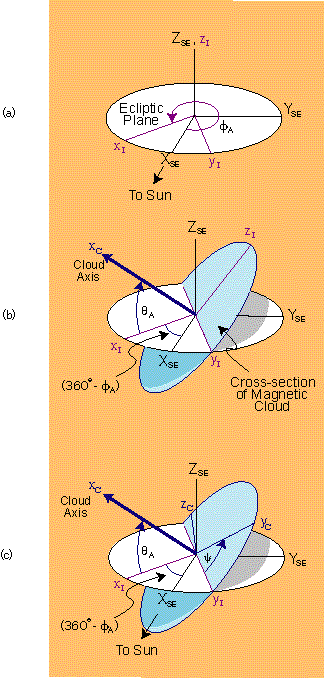
Graphic of cross section of a magnetic cloud

The figure shows the steps necessary to transform from a spacecraft- centered orthogonal Geocentric Solar Ecliptic coordinate system to an orthogonal magnetic cloud system, in which the x-axis is aligned with the magnetic cloud axis with positive polarity in the sense of the magnetic field along the axis (note that the orientation of the cloud axis in GSE coordinates is given by a longitude angle,Greek symbol Phi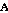Greek symbol Alpha, and a latitude angle, Greek symbol OmegaGreek symbol Alpha):


(a) The transformation from XGSE,YGSE,ZGSE (GSE, Geocentric Solar Ecliptic) to an Intermediate coordinate system xI,yI,zI, in which the zI  -axis is parallel to ZGSE, and the rotation about ZGSE is through the angle Greek symbol PhiA.


(b) The transformation from the xI,yI,zI system to a quasi-magnetic cloud system in which the xC-axis is aligned with the magnetic cloud axis. This transformation required a single rotation around the yI- axis through the angle Greek symbol OmegaA; this provides for the "tilt" of the cloud axis with respect to the Ecliptic plane. Note that the light blue plane is the cross­sectional plane of the magnetic cloud. Finally,


(c) The rotation about the cloud axis (xC) through an arbitrary angle 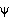Greek symbol Psi, so that the yC­axis is placed along some useful direction. The magnetic cloud axis system is then, xC,yC,zC, where zC = xC × yC, as usual.


Then the matrix that corresponds to the general transformation (arbitrary ) from GSE coordinate system to the magnetic cloud system has the following 9 elements (mij, where the subscripts i and j represent row and column, respectively):



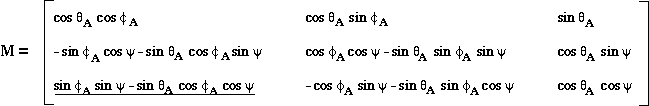
Matrix


If one chooses to arrange the yC-axis to be along a line (perpendicular to the cloud's axis) that goes from the center of the magnetic cloud to the observing spacecraft at the time of closest approach to the cloud axis, then ψ is related to 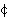Greek symbol PhiA and Greek symbol OmegaA in the following way:


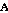ψ = tan-1(-tanGreek symbol PhiGreek symbol Alpha / sinGreek symbol OmegaGreek symbol Alpha),

but this line can be either the +yc axis or -yc axis.

 

 
To choose which sign is appropriate for any given case, we examine the sign of the matrix element of row 3, column 1 above; we call this element k (shown underlined above).  If k is < 0, then we set:

 

ψ = ψ + 180°, otherwise ψ remains its original value.

 

For some studies this particular definition and phasing of the yC -axis is useful. It ensures, for example, that while the spacecraft travels through the magnetic cloud it does so at a constant yC  -value at all times, in the magnetic cloud coordinate frame, and that the projection of the spacecraft's trajectory (+zc) on the cloud's cross-section will have a POSITIVE component along XGSE.